
This notebook contains an excerpt from the Python Programming and Numerical Methods - A Guide for Engineers and Scientists, the content is also available at Berkeley Python Numerical Methods.
The copyright of the book belongs to Elsevier. We also have this interactive book online for a better learning experience. The code is released under the MIT license. If you find this content useful, please consider supporting the work on Elsevier or Amazon!
< 21.4 Simpson’s Rule | Contents | 21.6 Summary and Problems >
Computing Integrals in Python¶
The \(scipy.integrate\) sub-package has several functions for computing integrals. The \(trapz\) takes as input arguments an array of function values \(f\) computed on a numerical grid \(x\).
TRY IT! Use the \(trapz\) function to approximate \(\int_{0}^{\pi}\text{sin}(x)dx\) for 11 equally spaced points over the whole interval. Compare this value to the one computed in the early example using the Trapezoid Rule.
import numpy as np
from scipy.integrate import trapz
a = 0
b = np.pi
n = 11
h = (b - a) / (n - 1)
x = np.linspace(a, b, n)
f = np.sin(x)
I_trapz = trapz(f,x)
I_trap = (h/2)*(f[0] + 2 * sum(f[1:n-1]) + f[n-1])
print(I_trapz)
print(I_trap)
1.9835235375094542
1.9835235375094546
Sometimes we want to know the approximated cumulative integral. That is, we want to know \(F(X) = \int_{x_0}^X f(x) dx\). For this purpose, it is useful to use the \(cumtrapz\) function \(cumsum\), which takes the same input arguments as \(trapz\).
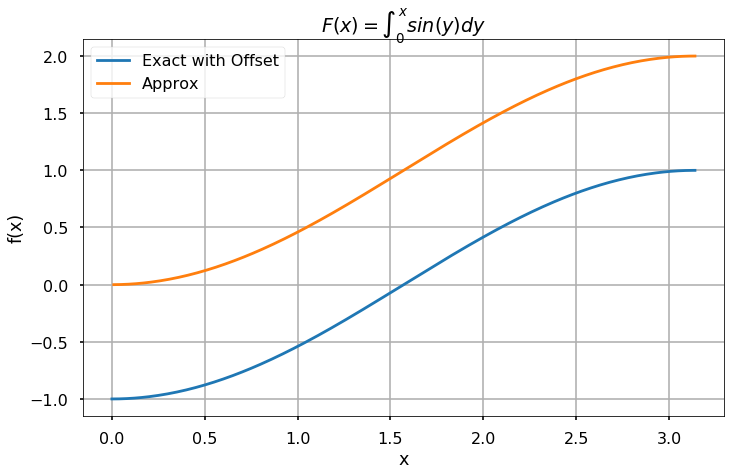
TRY IT! Use the \(cumtrapz\) function to approximate the cumulative integral of \(f(x) = \text{sin}(x)\) from \(0\) to \(\pi\) with a discretization step of 0.01. The exact solution of this integral is \(F(x) = sin(x)\). Plot the results.
from scipy.integrate import cumtrapz
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use('seaborn-poster')
x = np.arange(0, np.pi, 0.01)
F_exact = -np.cos(x)
F_approx = cumtrapz(np.sin(x), x)
plt.figure(figsize = (10,6))
plt.plot(x, F_exact)
plt.plot(x[1::], F_approx)
plt.grid()
plt.tight_layout()
plt.title('$F(x) = \int_0^{x} sin(y) dy$')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend(['Exact with Offset', 'Approx'])
plt.show()
The \(quad(f,a,b)\) function uses a different numerical differentiation scheme to approximate integrals. \(quad\) integrates the function defined by the function object, \(f\), from \(a\) to \(b\).
TRY IT! Use the \(integrate.quad\) function to compute \(\int_{0}^{\pi} \text{sin}(x)dx\). Compare your answer with the correct answer of 2.
from scipy.integrate import quad
I_quad, est_err_quad = \
quad(np.sin, 0, np.pi)
print(I_quad)
err_quad = 2 - I_quad
print(est_err_quad, err_quad)
2.0
2.220446049250313e-14 0.0
< 21.4 Simpson’s Rule | Contents | 21.6 Summary and Problems >
