
This notebook contains an excerpt from the Python Programming and Numerical Methods - A Guide for Engineers and Scientists, the content is also available at Berkeley Python Numerical Methods.
The copyright of the book belongs to Elsevier. We also have this interactive book online for a better learning experience. The code is released under the MIT license. If you find this content useful, please consider supporting the work on Elsevier or Amazon!
< CHAPTER 20. Numerical Differentiation | Contents | 20.2 Finite Difference Approximating Derivatives >
Numerical Differentiation Problem Statement¶
A numerical grid is an evenly spaced set of points over the domain of a function (i.e., the independent variable), over some interval. The spacing or step size of a numerical grid is the distance between adjacent points on the grid. For the purpose of this text, if \(x\) is a numerical grid, then \(x_j\) is the \(j^{\mathrm{th}}\) point in the numerical grid and \(h\) is the spacing between \(x_{j-1}\) and \(x_j\). The following figure shows an example of a numerical grid.
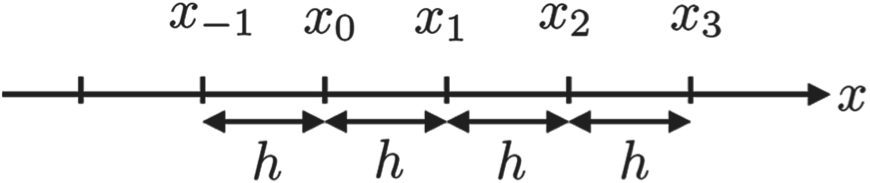
There are several functions in Python that can be used to generate numerical grids. For numerical grids in one dimension, it is sufficient to use the linspace function, which you have already used for creating regularly spaced arrays.
In Python, a function \(f(x)\) can be represented over an interval by computing its value on a grid. Although the function itself may be continuous, this discrete or discretized representation is useful for numerical calculations and corresponds to data sets that may be acquired in engineering and science practice. Specifically, the function value may only be known at discrete points. For example, a temperature sensor may deliver temperature versus time pairs at regular time intervals. Although temperature is a smooth and continuous function of time, the sensor only provides values at discrete time intervals, and in this particular case, the underlying function would not even be known.
Whether \(f\) is an analytic function or a discrete representation of one, we would like to derive methods of approximating the derivative of \(f\) over a numerical grid and determine their accuracy.
< CHAPTER 20. Numerical Differentiation | Contents | 20.2 Finite Difference Approximating Derivatives >
